凸包

前置知识

凸多边形与凸包

在了解凸包之前需要先了解凸多边形 (Convex Polygon)。直观的来看，一个凸多边形就是没有任何凹陷位的多边形，例如三角形、正方形、平行四边形、正五边形、正六边形等等。但是下面的这个“凸”字形却并非凸多边形，因为箭头所指之处实际是一个凹陷位。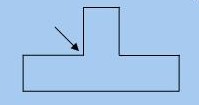

在数学上，凸多边形有另一个严格的定义。假设在一个多边形上（包括多边形的边界及边界围封的区域）任意取两点，并以一条线连接该两点，如果线段上的每一点，均在该多边形上，那么我们便认为这个多边形是凸多边形。
根据上述定义，便可以判断“凸”字形并非凸多边形，下图连接 A、B 点的线段有一部分并不在该多边形上。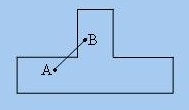

凸包概念

在了解了凸多边形之后，便可深入凸包 (Convex Hull)了。给定平面上的一个有限点集，这个点集的凸包就是包含点集中所有点的最小面积的凸多边形。用不严谨的话来讲，给定二维平面上的点集，凸包就是将最外层的点连接起来构成的凸多边型，它能包含点集中所有的点。
例如下图的点集共包含了12个点，图中的五边形便是该点集的凸包，构成五边形的五个点称为“凸包上的点”，其余点并非“凸包上的点”。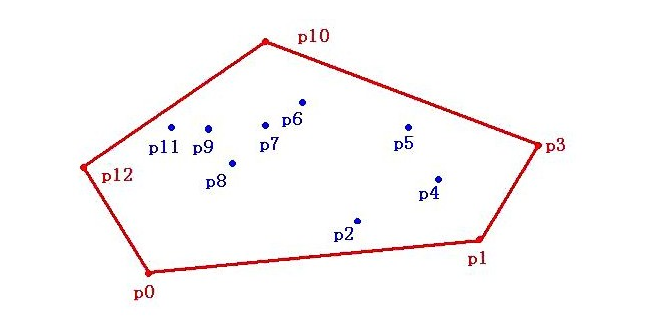

向量叉乘

定义

$$\vec C = \vec A \times \vec B$$
向量的叉乘，即求同时垂直两个向量的向量，即$\vec C$垂直于$\vec A$，且$\vec C$垂直于$\vec B$。
假设向量 $\vec A=(a.x, a.y, a.z),\vec B=(b.x, b.y, b.z),\vec C=(c.x, c.y, c.z)$，则
$$\vec C = \vec A \times \vec B = (a.y * b.z - a.z * b.y, a.z * b.x - a.x * b.z, a.x * b.y - a.y * b.x)$$
参考下图：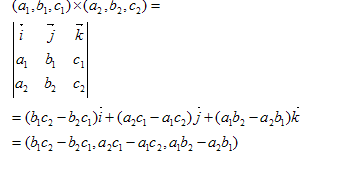

几何意义

$$|C| = |A| \times |B| = |A|\cdot|B|\cdot \sin\theta$$
$\theta$ 为两向量的夹角，$|C|$ 为两向量构成的平行四边形的面积。

应用

假设有两个二维向量$\vec A$、$\vec B$，可以直接把他们视作三维向量（a.z = b.z = 0）
此时，$\vec A$、$\vec B$ 的叉乘结果为
$$|C| = |A| \times |B| = (0, 0, a.x * b.y - a.y * b.x)$$
令$k = c.z = a.x * b.y - a.y * b.x$
可以由 $k$ 得到：

1. 计算 $\vec A$、$\vec B$ 向量构成的平行四边形的面积。
   向量 $\vec A$、$\vec B$ 的叉乘的模等于由 $\vec A$、$\vec B$ 组成的平行四边形的面积。
2. 判断旋转角度。
   如果 $k>0$时，那么$\vec A$正旋转到$\vec B$的角度为<180°，即$\vec B$在$\vec A$左侧；
   如果 $k<0$，那么$\vec A$正旋转到$\vec B$的角度为>180°；
   如果 $k=0$，那么$\vec A$、$\vec B$向量平行。

算法介绍

Graham扫描法

思路：先找到凸包上的一个点，然后从那个点开始按逆时针方向逐个找凸包上的点，实际上就是进行极角排序，然后对其查询使用。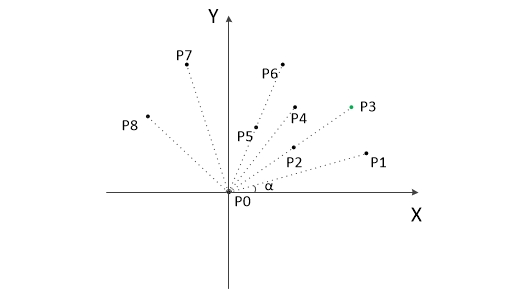

实现步骤：

1. 把所有点放在二维坐标系中，则纵坐标最小的点一定是凸包上的点，如图中的P0。
2. 把所有点的坐标平移一下，使 P0 作为原点，如上图。
3. 计算各个点相对于 P0 的幅角 α ，按从小到大的顺序对各个点排序。当 α 相同时，距离 P0 比较近的排在前面。例如上图得到的结果为 P1，P2，P3，P4，P5，P6，P7，P8。我们由几何知识可以知道，结果中第一个点 P1 和最后一个点 P8 一定是凸包上的点。
4. 连接P0和栈顶的那个点，得到直线 L 。看当前点是在直线 L 的右边还是左边。如果在直线的右边就执行步骤5；如果在直线上，或者在直线的左边就执行步骤6。
5. 如果在右边，则栈顶的那个元素不是凸包上的点，把栈顶元素出栈。执行步骤4。
6. 当前点是凸包上的点，把它压入栈，执行步骤7。
7. 检查当前的点 P2 是不是步骤3那个结果的最后一个元素。是最后一个元素的话就结束。如果不是的话就把 P2 后面那个点做当前点，返回步骤4。

最后，栈中的元素就是凸包上的点了。
下图为用 Graham 扫描法求解的过程：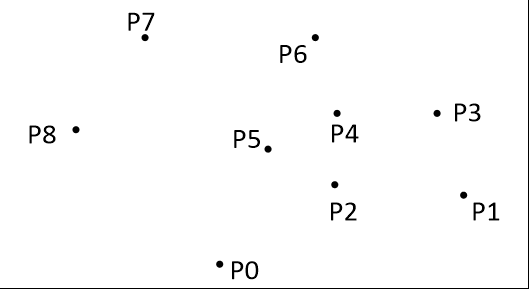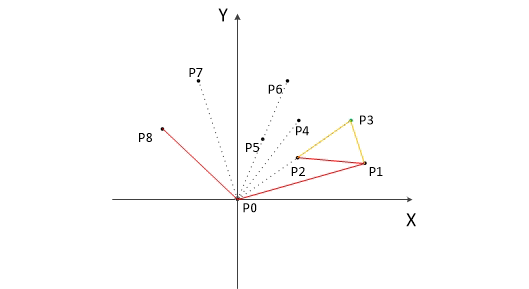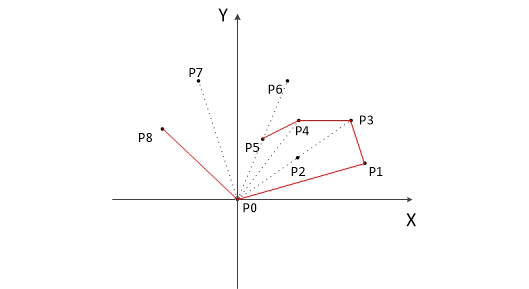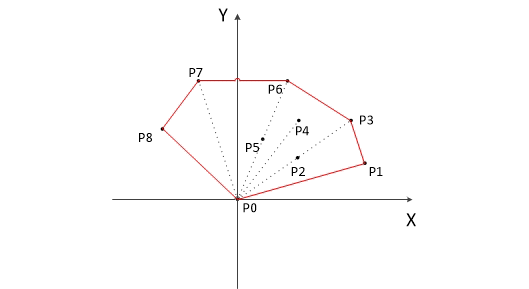

代码实现

赶时间，实在是不想写了😤。直接 copy 现成的代码，出处见结尾参考链接3。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

int cross(const std::vector<int>& p, const std::vector<int>& x, const std::vector<int>& y) {//计算向量px × py， 当返回值大于0时点y在向量px左边
	return (x[0] - p[0]) * (y[1] - p[1]) - (x[1] - p[1]) * (y[0] - p[0]);
}
 
std::vector<std::vector<int>> Graham(std::vector<std::vector<int>>& points) {
	int n = points.size(), p0 = 0;
	if (n <= 3)return points;//当n小于等于3时直接返回
	for (int i = 1; i < n; i++) {//寻找p0
		if (points[i][1] < points[p0][1]) p0 = i;
		else if (points[i][1] == points[p0][1] && points[i][1] < points[p0][1]) p0 = i;
	}
	std::vector<int> t = points[0];
	points[0] = points[p0];
	points[p0] = t;
	t = points[0];
	sort(points.begin() + 1, points.end(), [t](const std::vector<int>& a, const std::vector<int>& b)->bool {
		int k = cross(t, a, b);
		if (k == 0)return (a[0] - t[0]) * (a[0] - t[0]) + (a[1] - t[1]) * (a[1] - t[1]) < (b[0] - t[0]) * (b[0] - t[0]) + (b[1] - t[1]) * (b[1] - t[1]);//当叉积为0时证明t, a, b在同一条直线上，此时与t距离更小的点排在前面
		return k > 0;//当叉积大于0时a到t的极角要小于b到t的极角
		});
	std::vector<std::vector<int>> S;
	S.emplace_back(points[0]);
	S.emplace_back(points[1]);
	S.emplace_back(points[2]);
	int size = 3;//栈的大小
	for (int i = 3; i < n; i++) {
		//对于求凸包，可能凸包的一条边上包含多个顶点，有的题需要把所有顶点都算入凸包，有的题只需考虑两个端点，若只需考虑两个端点，把下边的<换成<=即可
		while (cross(S[size - 2], S[size - 1], points[i]) < 0) {
			size--;
			S.pop_back();
		}
		S.emplace_back(points[i]);
		size++;
	}
	//由于当有顶点和p0pn-1共线时（即p0和排序后的最后一个点），我们的算法会漏掉这些点，所以需要单独考虑
	for (int i = n - 2; i >= 0; i--) {
		if (cross(points[0], points[n - 1], points[i]) == 0 && S.size() < n)S.emplace_back(points[i]);//加上S.size() < n是为了防止那些恶心的所有点共线的测试案例
		else break;
	}
	return S;
}

效果展示

参考链接

• 参考链接1
• 参考链接2
• 参考链接3
• 参考链接4
• 参考链接5
• 参考链接6