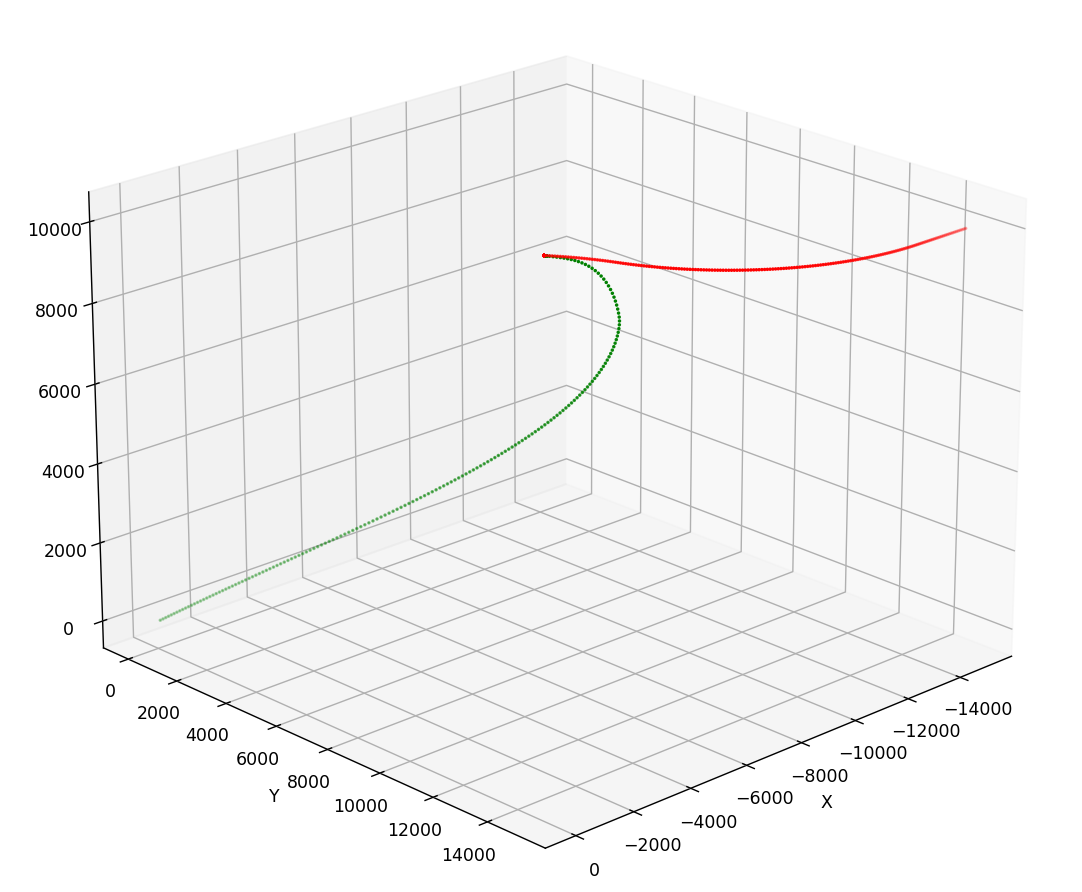
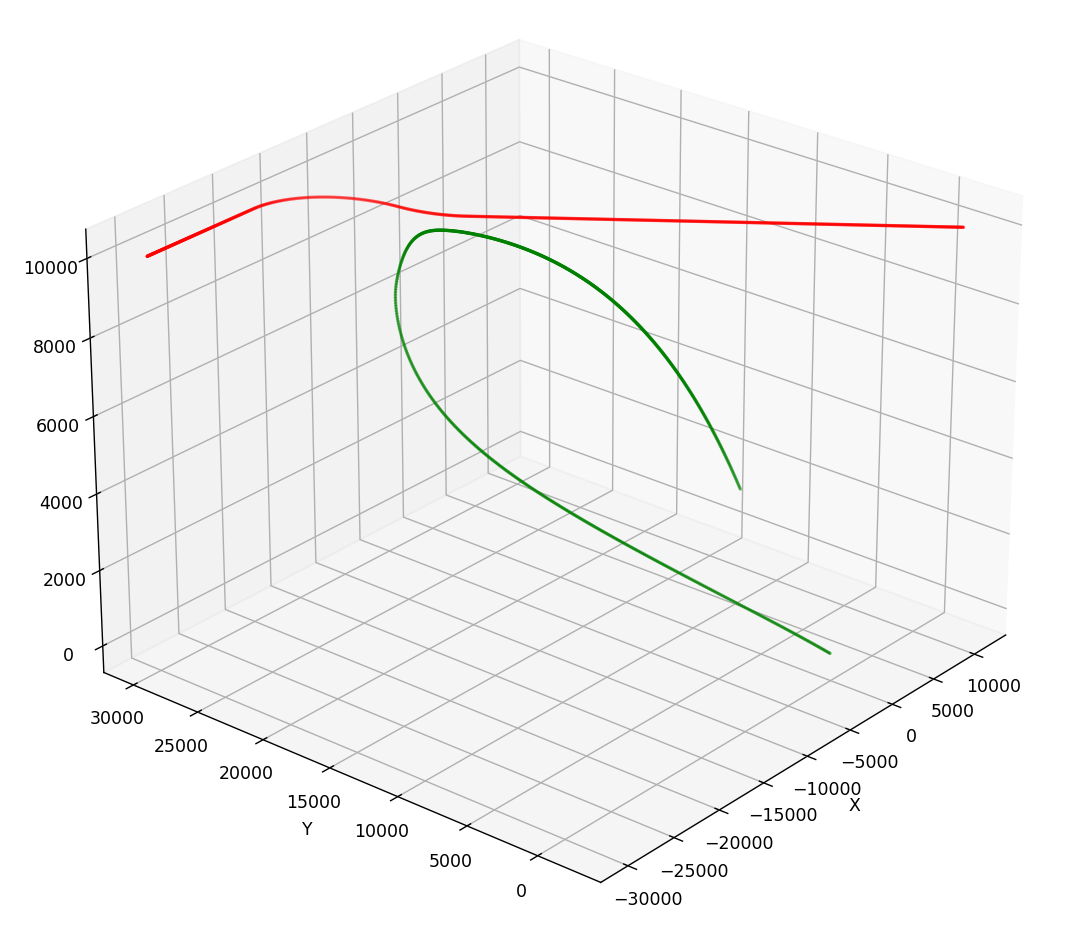
仿真演示导弹击落飞行目标
仿真演示导弹击落飞行目标
参数限制条件
- 飞行器目标可设定高度5-20km,飞行速度400-800m/s,速度大小不变;但可在飞行水平面机动,机动转向最大速度为0.1rad/s;
- 导弹初速800m/s,风阻f=-bV, b=0.02m,m为导弹质量;重力加速度9.81m/s^2;
- 导弹点火提供前进方向推进力,单次推进可持续2s:f=ma, a=100m/s^2;最多可以提供3次点火推进;
- 导弹基地雷达感知范围40km,飞行器感知导弹范围为20km,导弹进入该范围即启动机动规避;
- 飞行目标可以在飞行平面转向,转向最大速度为0.1rad/s;不考虑飞行目标垂直方向机动。
导弹算法部分
导引律
导引律是用来引导飞行器到目的点或与目标相遇的算法。在本项目中,导弹的导引律使用了比例导引法,其核心思想是导弹飞行过程中,导弹速度向量的转动角速度与目标视线的转动角速度成比例。
比例导引法导引关系式:
$$\frac{d\sigma}{dt} - K\frac{dq}{dt} = 0$$
核心实现代码如下:
1 | void MissileControl() |
当飞行器直线飞行,导弹的轨迹如下所示。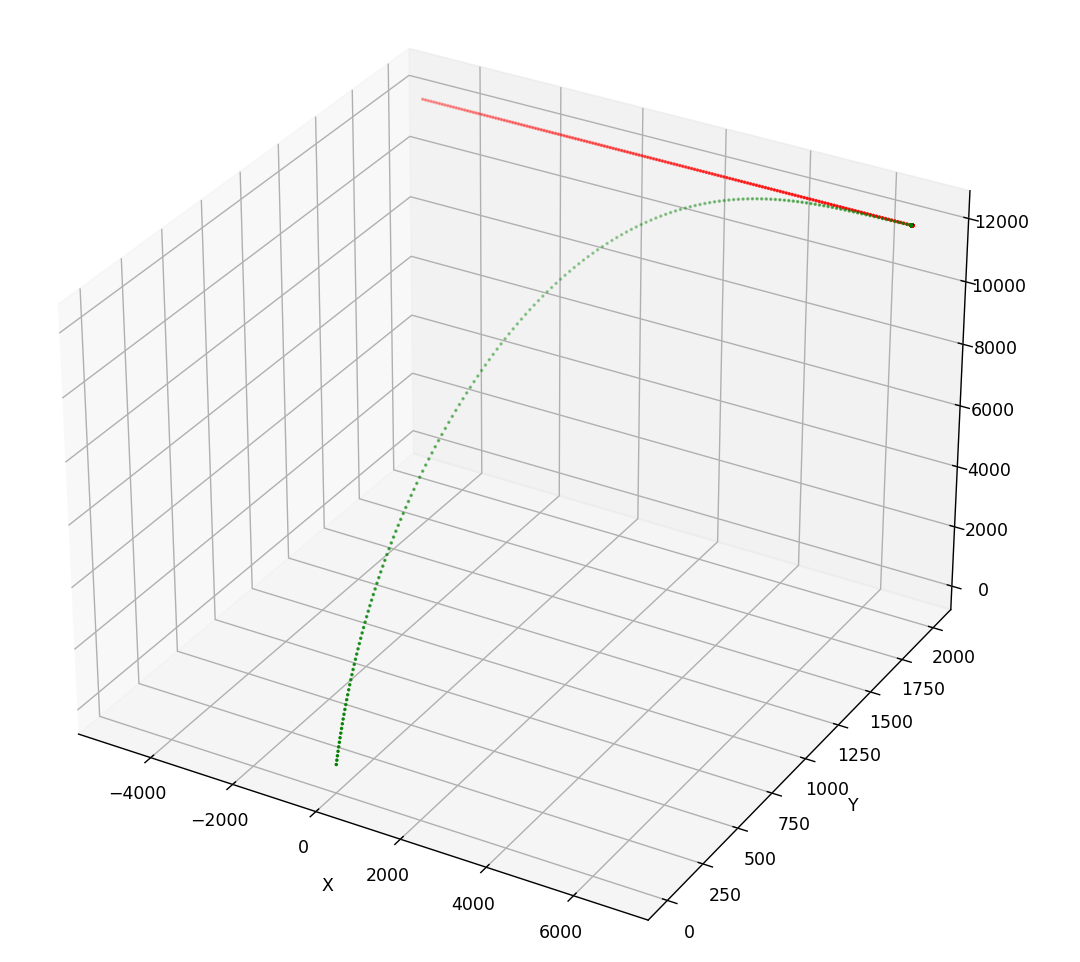
点火策略
导弹点火提供前进方向推进力,最多可以提供3次点火推进。在导弹刚起飞时,记录下此时导弹与飞行器的最大距离,并且在此点火第一次。
当运行到两者的距离达到之前记录的最大距离一半时,如果当前没有加速,进行第二次点火;如果正在加速,则等待加速完毕再点火。同时更新最大距离为当前的距离。
按照上述流程再进行第三次点火。并且,如果当垂直方向的速度分量小于100米每秒时,就会进行一次点火补充垂直速度。核心代码如下。
1 | if (distance < 0.5 * max_dis && Missile.if_speedup == 0) // 一半路程且未加速 |
飞行器算法部分
根据美国空军基本战斗机动BFM的描述,当遭遇导弹威胁时,用方位角对付导弹。当导弹飞向你,要尽快转弯,使导弹在你的 3/9 线上,给导弹制造最大的制导难题。导弹要击中你需要按照提前量飞行,而你这样就使导弹的提前量最大。而且你会以最大视线率穿越导弹的制导头视野。
简单来说,就是尽量要让导弹时刻处于飞机的3点钟或者9点钟方向,使导弹的提前量达到最大。所以,要尽量让导弹的位置距离机头和机尾的距离相同,此时的导弹一定位于飞机的3点钟或者9点钟方向。核心代码如下所示。
1 | double temp_angle; // 方位角 |
实现飞机的轨迹控制也很简单,在机器人运动学里,只需角速度和线速度便可实现平面内的轨迹控制。而飞行器的高度是固定的,不考虑垂直面的机动,所以可以直接用一个角速度和线速度来控制轨迹。其中,V 和 W 分别表示飞行器的线速度和角速度。当角速度不为 0 时,飞行器作圆周运动;当角速度为 0 时,飞行器作直线运动。W 也是有方向的,逆时针为正,顺时针为负。通过控制 W 和 V 就可以控制飞行器轨迹。核心代码如下。
1 | Aerocraft.pos_x = Aerocraft.pos_x + cos(Aerocraft.angle) * Aerocraft.speed * TIME; |
对抗条件
在同一规避算法下,不同的速度、高度和距离都会产生不同效果。
速度
在速度不同,其他条件相同的情况下。速度越低越容易被击落。下图上边速度为500,下边速度为700。
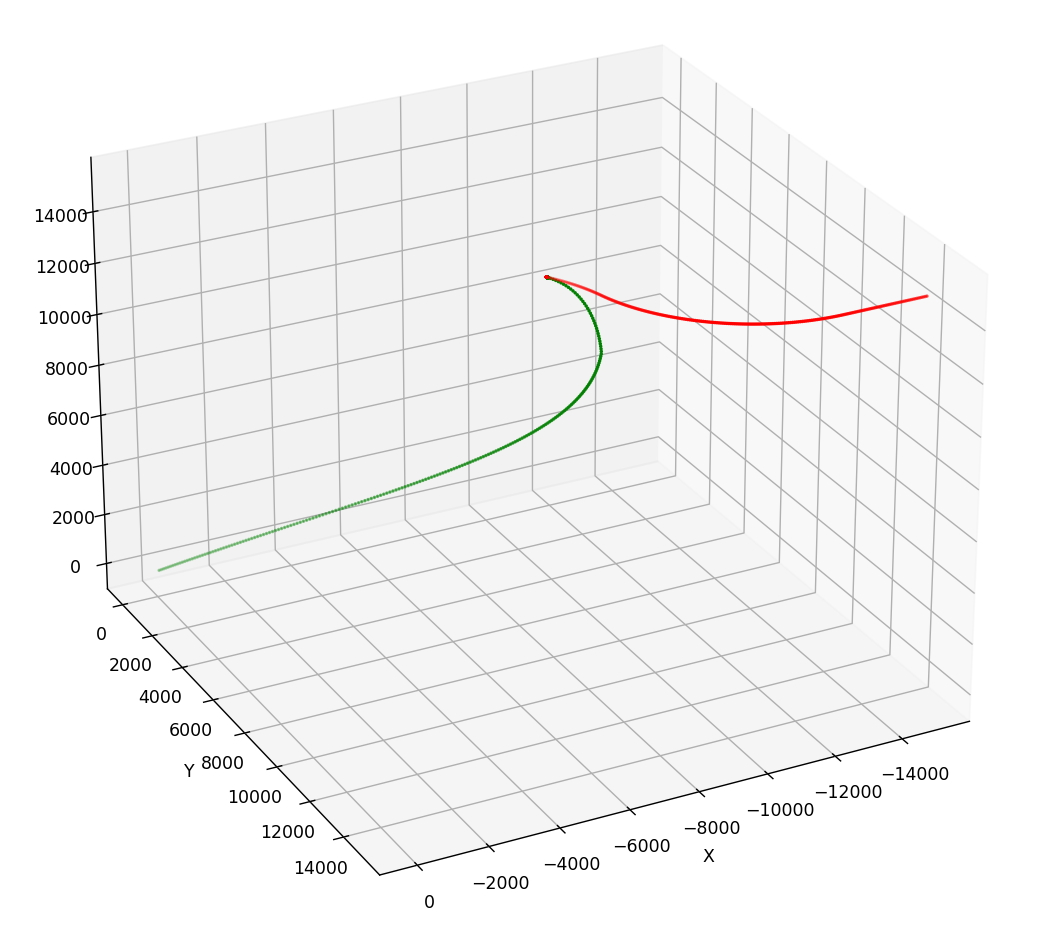
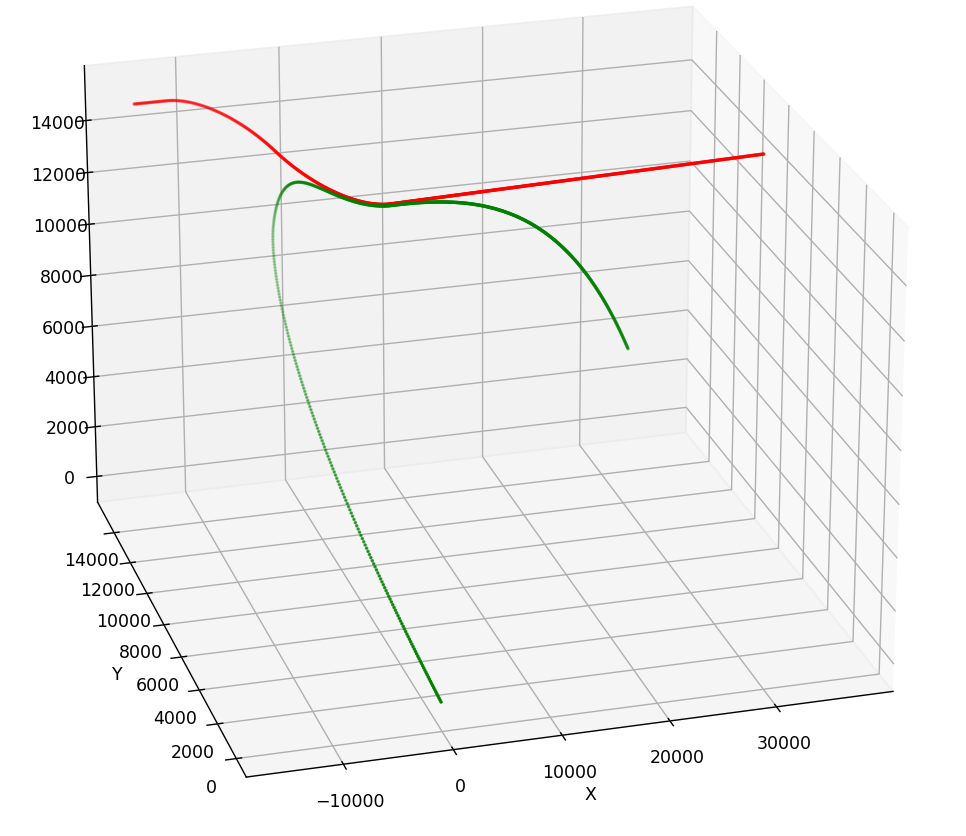
高度
在高度不同,其他条件相同的情况下。高度越低越容易被击落。上边高度为10km,下边高度为20km.
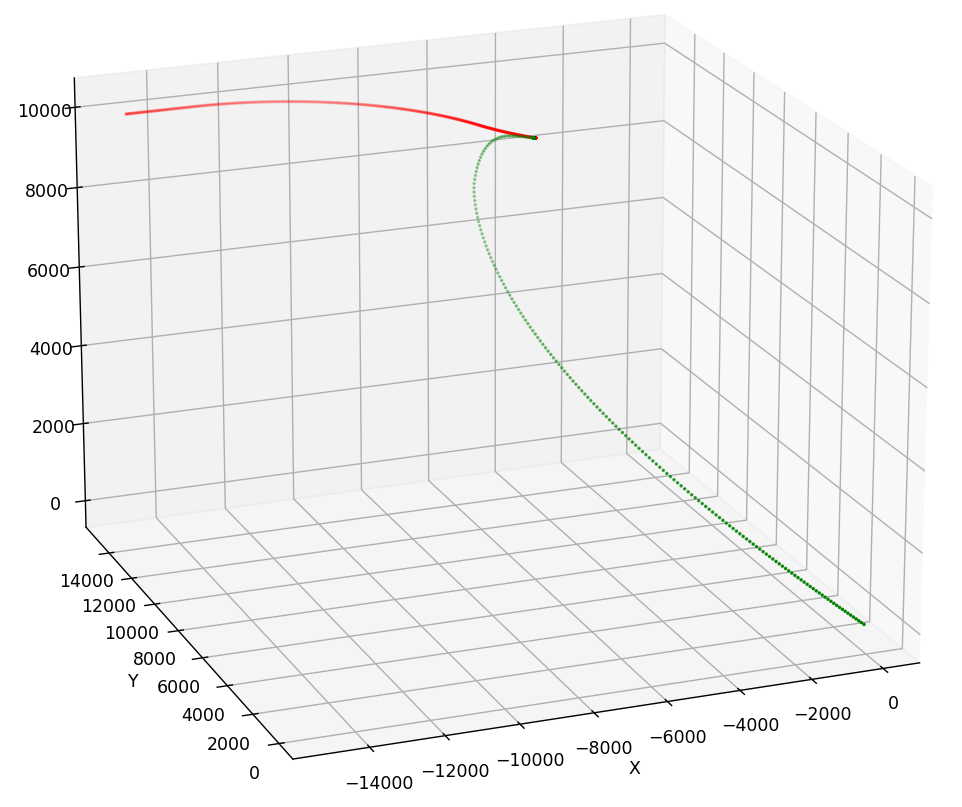
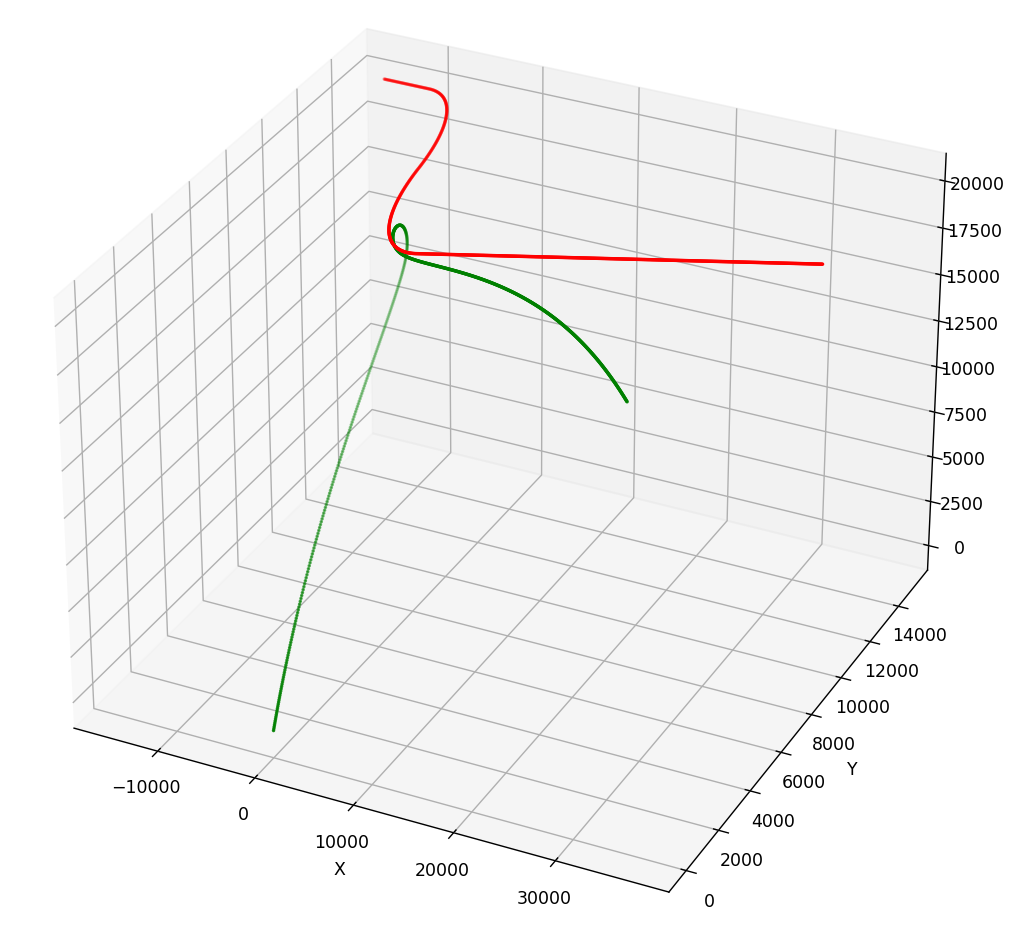
距离
在距离不同,其他条件相同的情况下。距离越近越容易被击落。上边距离为15km,下边距离为30km.