轨迹规划
轨迹规划
介绍
最近在搞大学的最后一门课设,其中一个项目内容是“仿真演示导弹击落飞行目标的过程”,要为地对空导弹设计追踪算法,为飞行目标设计机动规避算法并且进行对抗。其中飞行器的的参数如下:
- 高度5-20km
- 飞行速度400-800m/s,速度大小不变
- 机动转向最大速度为0.1rad/s
- 不考虑飞行目标垂直方向机动
飞机规避导弹按照最大角速度转向时,因为速度大小不变,就相当于一个匀速圆周运动,可以用物理方法或几何方法来实现画圆。
几何方法
当初想使用几何方法其实是对条件理解错了😂,以为机动转向最大速度是飞行器绕外部一点旋转的角速度,查了资料才发觉其实应该是偏航角速度。
但无论如何,用几何方法模拟圆周运动还是很简单的。照着下面公式代入就行。
$$x_1 = x_0 + r * cos(\alpha)$$
$$y_1 = y_0 + r * sin(\alpha)$$
物理方法
由于不考虑飞行目标垂直方向机动,只在二维平面上运动,所以只用 x、y 两个轴就可以表示飞行器的坐标。由于飞机的转向速度受限,用 $\theta$ 来表示飞行器的速度方向,则其运动约束为:
$$ \dot x \sin \theta- \dot y \cos \theta = 0$$
在此约束条件下,飞行器的运动学模型可以用下式表示:
$$\dot x = v \cos \theta$$
$$\dot y = v \sin \theta$$
$$\dot \theta = \omega$$
其中,$v$ 和 $\omega$ 分别表示飞行器的线速度和角速度。当角速度不为 0 时,飞行器作圆周运动;当角速度为 0 时,飞行器作直线运动。$\omega$也是有方向的,逆时针为正,顺时针为负。通过控制 $\omega$ 和 $v$ 就可以控制飞行器轨迹。
代码实现如下:
1 | // 飞行器以 0.1rad/s 逆时针旋转 |
TIME 为时间步长,越小精度越高。
实现效果如下: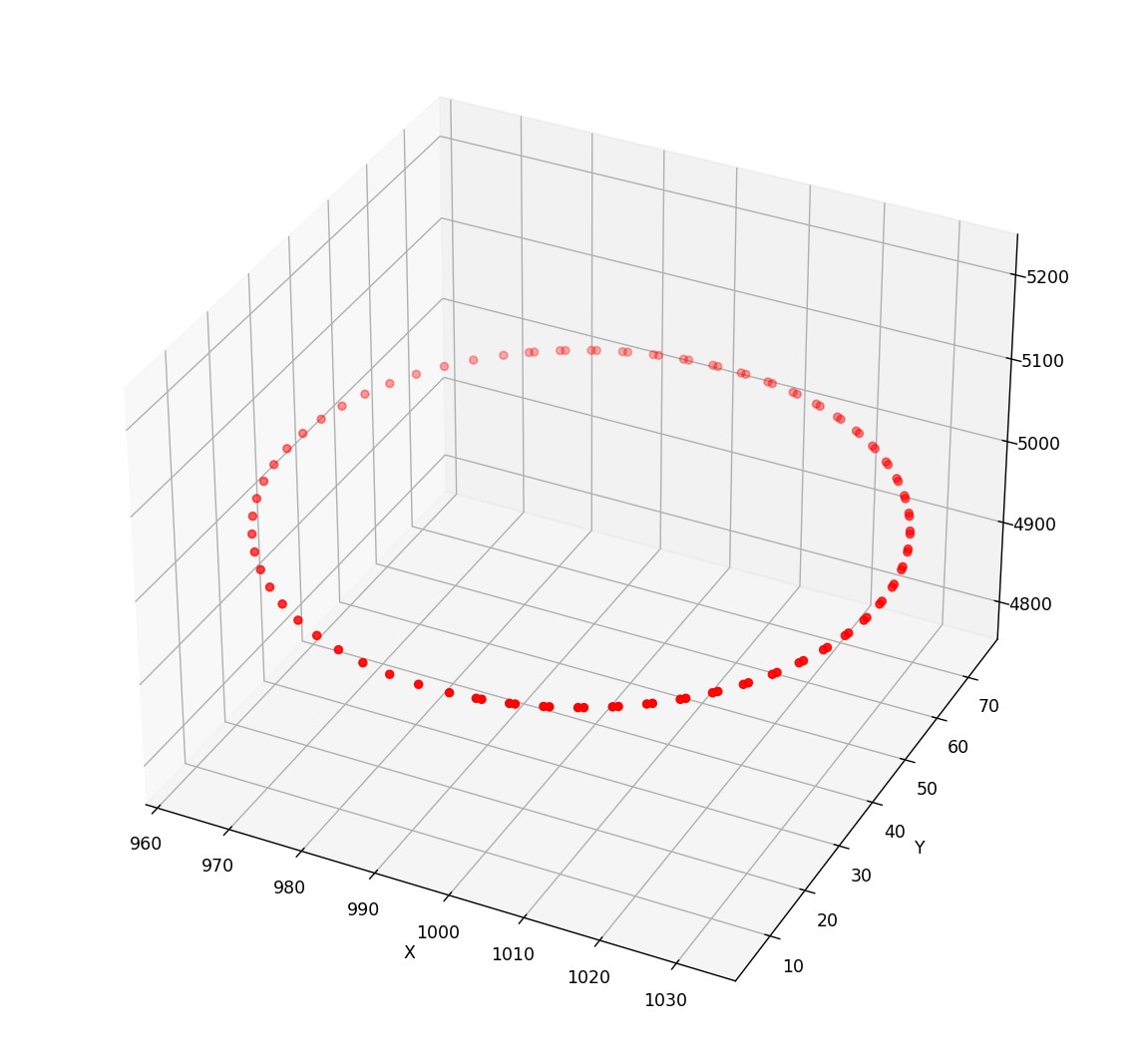
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 Star!








